Simulating Covid-19 Vaccine Data using a Discrete-Time Simulation

Introduction

This vignette contains an in-depth example on how to use the sim_discrete_time() function to generate complex time-to-event data. Unlike the other vignettes, we will not rely on a overly simple example here. Instead, our aim is to generate somewhat realistic data about the Covid-19 pandemic. In particular, we are interested in generating a longitudinal data set containing Covid-19 infections, vaccines and adverse side effects of those vaccines. The aim of the real study was to create a data set that is reasonably close to real data, including measurement problems as described below. This data generation algorithm was then used to identify a suitable data analysis strategy for the real data. We only describe a slightly simplified version of the data generation part here to give a detailed example on how the sim_discrete_time() function may be used effectively.

Note that the algorithm described here is not completely the same as the one we originally used, because that would require us to include confidential data into this vignette, which is sadly impossible.

We also strongly recommend reading the other two vignettes of this package first.

How to get started

Simulating data that is reasonably close to a complex real system is not a trivial task, even when using this package. Dividing the big task of obtaining a valid data generation model into multiple sub-tasks is a great first step in the right direction. We suggest following the 7 steps below:

1.) Formulate the goal of your research project in a detailed fashion.

If you haven’t done this yet, now is the time. Try to make your goal as explicit as possible. This will help you in deciding which aspects of the system are important to you and which can be safely ignored.

2.) Build a theoretical model of the system you want to simulate.

This entails reading up on relevant literature and writing down any assumptions you may already have about the system. Perhaps (and usually most likely) other researchers have tried to build a simulation model for the same system (or a very similar system). A great way to encode your causal assumptions of the system is time-dependent DAG, as discussed in the other vignettes.

3.) Identify the parts of the system that you are most interested in.

Real systems are incredibly complex. Any simulation will have to make some simplifying assumptions. After building a moderately detailed version of the theoretical model, you will have to decide which aspects are of interest to your research project and which aren’t.

4.) Obtain and analyze real data.

If the simulated data should correspond to real data, it is crucial to base the input of the model on actual empirical data. Using the empirical data, you may be able to derive appropriate distributions for the root nodes and appropriate functional forms of the relationship between the considered variables.

5.) Simulate data for $t = 0$ (if needed).

After having specified suitable distributions and relationships, generate the initial data used in the simulation process. It is important to check this data thoroughly, as it will be used as a basis for all subsequent steps of the simulation. The sim_from_dag() function might be very helpful for this step.

6.) Write functions for each time-varying node, one at a time.

Each time-varying node requires a user written function that transforms the data at $t$ to the data at $t + 1$ . It might be helpful to add one time-varying node at a time and proceeding to step 7.) before adding other variables, if possible.

7.) Inspect the resulting data for inconsistencies.

Validating your simulation code is important to ensure that no mistakes slipped through. This may be done by fitting models relying on your modeling assumptions to the generated data and checking whether those models produce the expected results.

Our research goal and the theoretical model

Since this vignette is mostly concerned with the practical implementation of the discrete-time simulation approach using this R-package, we will not spend too much time on the first 4 steps of the process mentioned in the previous section. We only briefly present the most important points.

Research goal

Our actual research goal was to identify a suitable data analysis strategy for the assessment of Covid-19 vaccine side-effects for a particular real-life data set. To do this we decided to simulate data that is as close to the real data as possible. Using this data we could then try out different analysis strategies and see which one performed adequately. The goal for this vignette is to use parts of this model to showcase the capabilities of the simDAG package. More information on the actual simulation can be found in the first related publication (Denz et al. 2023).

Theoretical model

There is a seemingly endless amount of literature describing models for the Covid-19 pandemic and the associated Covid-19 vaccines. Trying to include all relevant aspects would be an unfeasible task. After deliberating on this literature we decided to include only a few key variables. To make this vignette readable we further limited the variables to only include the most essential:

vaccination: The time at which the person received the first vaccine.
covid: Whether a Covid-19 infection occurred.
sickness: Whether the person has developed the sickness of interest.

We assume that these three variables vary over time and cause each other.

Implementing the model

Instead of diving in deep from the start and trying to include all relevant variables with all relevant relationships at once, it is often better to build a very simplified version first and to start adding more and more stuff to it as we continue.

Part 1: Adding vaccination, covid and sickness

The most important variables for us are the vaccination, the covid-19 infection and the sickness. All of these are variables that have a certain probability of occurrence at each point in time. Once they occur, they last for some duration (e.g. someone being sick for two weeks or something similar). After the event is over, there is usually some duration where the person is “immune” to receiving the event again. This is a perfect case for using a time-dependent node of type "time_to_event".

We start out modeling every one of these variables as completely independent of each other using the following DAG:

library(data.table)
library(ggplot2)
library(simDAG)

dag <- empty_dag() +
  node_td("vaccination", type="time_to_event", prob_fun=0.001,
          event_duration=21, immunity_duration=Inf) +
  node_td("covid", type="time_to_event", prob_fun=0.001, event_duration=30,
          immunity_duration=80) +
  node_td("sickness", type="time_to_event", prob_fun=0.0001,
          event_duration=2, immunity_duration=2)

In the DAG above, we supplied a constant value to each of the prob_fun arguments, indicating that regardless of time and other variables, each event has a constant probability of occurring on each day. We set the event_duration of vaccination to 21, because we want to model the time after vaccination in which the risk for the adverse side-effect (e.g. the sickness) is higher than usual later on. By setting the immunity_duration of the vaccination to Inf, we are currently only allowing the person to get one vaccination over the entire time. The sickness is allowed to occur again directly after it was over.

Part 2: Adding adverse effects of vaccination and covid

We can make this data-generation process a little more interesting by making both the vaccination and covid have an effect on the probability of developing the sickness. We will do this by simply raising the probability of occurrence of the sickness by a constant factor whenever either a covid or vaccination event is currently happening. This can be done by formulating an appropriate prob_fun for the sickness node:

prob_sickness <- function(data, rr_covid, rr_vacc, base_p) {

  # multiply base probability by relevant RRs
  p <- base_p * rr_vacc^(data$vaccination_event) * rr_covid^(data$covid_event)

  return(p)
}

This works because any number to an exponent of 1 is itself, while any number to an exponent of 0 is one. The vaccination_event and covid_event columns are always either TRUE (when an event is currently happening) or FALSE (when no event is currently happening), which are interpreted as 1 and 0 by R. Let’s update our DAG:

dag <- empty_dag() +
  node_td("vaccination", type="time_to_event", prob_fun=0.001,
          event_duration=21, immunity_duration=Inf) +
  node_td("covid", type="time_to_event", prob_fun=0.001, event_duration=30,
          immunity_duration=80) +
  node_td("sickness", type="time_to_event", prob_fun=prob_sickness,
          parents=c("vaccination_event", "covid_event"),
          base_p=0.0001, rr_covid=3.5, rr_vacc=3.24,
          event_duration=2, immunity_duration=2)

Instead of passing a constant value to the prob_fun argument, we are now passing it the previously defined function. Because our function has base_p, rr_covid and rr_vacc as arguments without defaults, we have to specify those in the node_td call as well. We keep the original base_p, and set the relative risks to 3.5 and 3.24 respectively. Additionally, we have to set both the vaccination_event and the covid_event columns as parents now, because they are used in the prob_sickness function.

Part 3: Making the vaccine useful

So far we assumed that the covid infection probability is unaffected by whether the person received the vaccine or not. We will now change this by implementing a time-window after receiving the vaccine in which the person cannot develop a covid infection. Again, this can be done by defining an appropriate prob_fun function, this time for the covid node:

prob_covid <- function(data, base_p, vacc_duration) {
  
  p <- fifelse(data$vaccination_time_since_last < vacc_duration,
               0, base_p, na=base_p)
  return(p)
}

In this function we use the column vaccination_time_since_last, which is a column that can optionally be created in time-to-event nodes by setting time_since_last to TRUE. So let’s again update our DAG accordingly:

dag <- empty_dag() +
  node_td("vaccination", type="time_to_event", prob_fun=0.001,
          event_duration=21, immunity_duration=Inf,
          time_since_last=TRUE) +
  node_td("covid", type="time_to_event", prob_fun=prob_covid,
          parents=c("vaccination_time_since_last"),
          base_p=0.001, vacc_duration=80, event_duration=30,
          immunity_duration=80) +
  node_td("sickness", type="time_to_event", prob_fun=prob_sickness,
          parents=c("vaccination_event", "covid_event"),
          base_p=0.0001, rr_covid=3.5, rr_vacc=3.24,
          event_duration=2, immunity_duration=2)

Instead of just updating the parents and prob_fun arguments of the covid node, we now also had to set the time_since_last argument of the vaccination node to TRUE as well to get the required additional column. Our data-generation algorithm is getting better now. But there is still a lot we can do.

Part 4: Sick people don’t get vaccinated

In reality, very little people who were currently experiencing a Covid-19 infection went and got the vaccine. In fact, this is absolutely discouraged by doctors world-wide. To add this circumstance to the model, we once again simply have to update the probability of receiving a vaccination, by defining an appropriate prob_fun:

prob_vaccination <- function(data, base_p) {
  
  p <- fifelse(data$covid_event, 0, base_p)
  
  return(p)
}

Using this function, the probability of getting vaccinated for any individual that is currently experiencing a covid infection is 0. Let’s update our DAG one more time to include these changes:

dag <- empty_dag() +
  node_td("vaccination", type="time_to_event",
          prob_fun=prob_vaccination,
          parents=c("covid_event"), base_p=0.001,
          event_duration=21, immunity_duration=Inf,
          time_since_last=TRUE) +
  node_td("covid", type="time_to_event", prob_fun=prob_covid,
          parents=c("vaccination_time_since_last"),
          base_p=0.001, vacc_duration=80, event_duration=30,
          immunity_duration=80) +
  node_td("sickness", type="time_to_event", prob_fun=prob_sickness,
          parents=c("vaccination_event", "covid_event"),
          base_p=0.0001, rr_covid=3.5, rr_vacc=3.24,
          event_duration=2, immunity_duration=2)

Again we simply changed the prob_fun argument and added the correct parents to the appropriate node. Our final “DAG” looks like this:

plot(dag, mark_td_nodes=FALSE)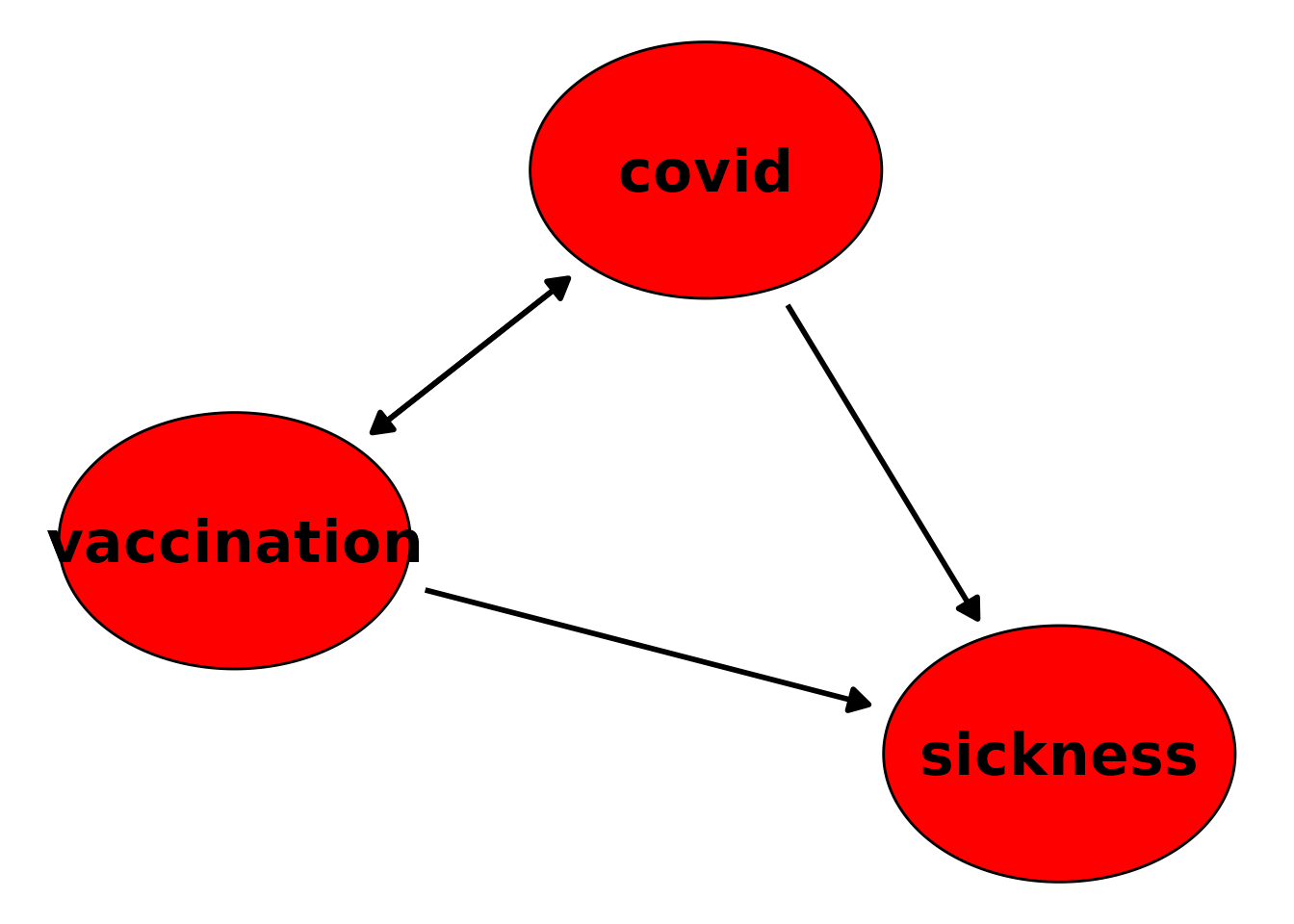
#> Loading required namespace: ggforce

Note that in this plot it doesn’t look like a classic DAG anymore, because it has a bi-directional arrow between covid and vaccination due to the time-dependent nature of their relationship.

Generating Data using the final model

Suppose we are now pleased with the complexity of our data-generation algorithm and want to simulate data from it. We can do this by simply calling the sim_discrete_time() function on the specified DAG:

set.seed(42)
sim <- sim_discrete_time(dag, n_sim=1000, max_t=800)
summary(sim)
#> A simDT object with:
#>   -  1000  observations
#>   -  800  distinct points in time
#>   -  3  time-varying variables in total
#>   -  3  time_to_event nodes
#>   -  0  competing_events nodes
#> Only the last state of the simulation was saved.

For exemplary purposes, we kind of arbitrarily used 1000 individuals and let the simulation run for 800 days. By calling the plot() method, we get a concise overview over the process we simulated:

plot(sim, box_text_size=4)

A more useful output of the resulting data can be obtained using the sim2data() function. For example, we could transform the output to the start-stop format:

sim2data(sim, to="start_stop")
#>         .id start  stop vaccination  covid sickness
#>       <int> <int> <num>      <lgcl> <lgcl>   <lgcl>
#>    1:     1     1   178       FALSE  FALSE    FALSE
#>    2:     1   179   199        TRUE  FALSE    FALSE
#>    3:     1   200   800       FALSE  FALSE    FALSE
#>    4:     2     1   501       FALSE  FALSE    FALSE
#>    5:     2   502   531       FALSE   TRUE    FALSE
#>   ---                                              
#> 3466:  1000     1    47       FALSE  FALSE    FALSE
#> 3467:  1000    48    49       FALSE  FALSE     TRUE
#> 3468:  1000    50   131       FALSE  FALSE    FALSE
#> 3469:  1000   132   152        TRUE  FALSE    FALSE
#> 3470:  1000   153   800       FALSE  FALSE    FALSE

As can be seen, we managed to implement a fairly complex data-generation mechanism using only a few small function definitions and a few lines of code, allowing us to generate a complex dataset with three interdependent time-varying variables with only minimal effort.

Going even further

There is no need to stop here. We could make this simulation model even more complex by implementing any of the following things:

Adding time-dependent base-probabilities for vaccination, covid and sickness
Adding different kinds of vaccinations, perhaps with different effects on covid and/or sickness
Adding time-fixed variables such as sex which have an effect on any of the other variables
Allowing multiple vaccinations
Changing the constant raising of the probabilities in the form of a relative risk to a more realistic non-linear time-dependent relative risk

There are of course many more possible extensions, all of which can be implemented by augmenting the respective prob_fun arguments and updating the dag accordingly. In fact, in the real monte-carlo simulation we conducted, that is exactly what we did. We used empirical data to model time-dependent base-probabilities and more. How much complexity you really need is completely up to you. We hope that the simDAG package can help you with whatever you need.

References

Banks, Jerry, John S. Carson II, Barry L. Nelson, and David M. Nicol (2014). Discrete-Event System Simulation. Vol. 5. Edinburgh Gate: Pearson Education Limited.

Denz, Robin, Katharina Meiszl, Peter Ihle, Doris F. Oberle, Ursula Drechsel-Bäuerle, Katrin Scholz, Ingo Meyer and Nina Timmesfeld (2023). “Impact of Record-Linkage Errors in Covid-19 Vaccine-Safety Analyses using German Health-Care Data: A Simulation Study”. In: arXiv:2310.15016

Robin Denz