Simulating Data using a Discrete-Event Approach
Robin Denz
Source:vignettes/v_sim_discrete_event.Rmd
v_sim_discrete_event.RmdIntroduction
In this small vignette, we introduce the
sim_discrete_event() function, which can be used to
generate complex longitudinal data with a continuous time scale based on
the discrete-event simulation (DES) framework (Banks et al. 2014). It is very similar to the
sim_discrete_time() function in spirit, but relies on a
completely different algorithm to generate the data. This algorithm is
usually much faster than the discrete-time approach, while also being
more precise. The drawback is some added complexity and a little less
flexibility. For example, in sim_discrete_event(),
continuous, categorical or count-based time-dependent variables are
currently not supported. Only binary variables added using the
"next_time" node type may be used.
The goal of the sim_discrete_event() function is not to
provide a general framework for DES. Multiple other R packages, such as
simmer (Ucar, Smeets, and Azcorra
2019; Degeling et al. 2025) and DES (Matloff 2017), as well as software packages
outside R have been developed for that purpose and are much more useful
in this regard. Instead, the aim of this function is to provide a
specific, but fairly general, DES model that may be used to generate
data from DAG based description of the data generation process (DGP). In
other words: if you want to perform a classic DES with interacting
agents using a classic simulation modeling approach, this is probably
not the right package for you. If you want to generate complex
time-dependent data based on a stochastic model, you have come to the
right place.
Throughout the vignette, we assume that the reader is already
familiar with the simDAG syntax. If this is not the case,
we recommend consulting the introductory vignette or the main paper
associated with this package first (Denz and
Timmesfeld 2025).
What is Discrete-Event Simulation and Why Use it?
In a discrete-event simulation (DES), the data is generated according
to a statistical model, which describes a system as a sequence of
distinct (or discrete) events that happen in continuous time and may
influence each other. Any DES starts with the generation of
individuals at
that have some characteristics, such as values of multiple covariates.
The full description of all individuals is considered to be the
state of the simulation here. This state only ever
changes when some event occurs. A simple example for an
event would be a variable changing its value from
FALSE to TRUE or vice versa. If such an event
occurs, the time of the simulation is advanced to the timing of this
event. The state of the simulation is then updated to reflect the
changes brought on by this event. Next, the time until the next event is
generated and the process is repeated until some condition is met. The
flowchart below gives a generalized description of a DES as considered
here.
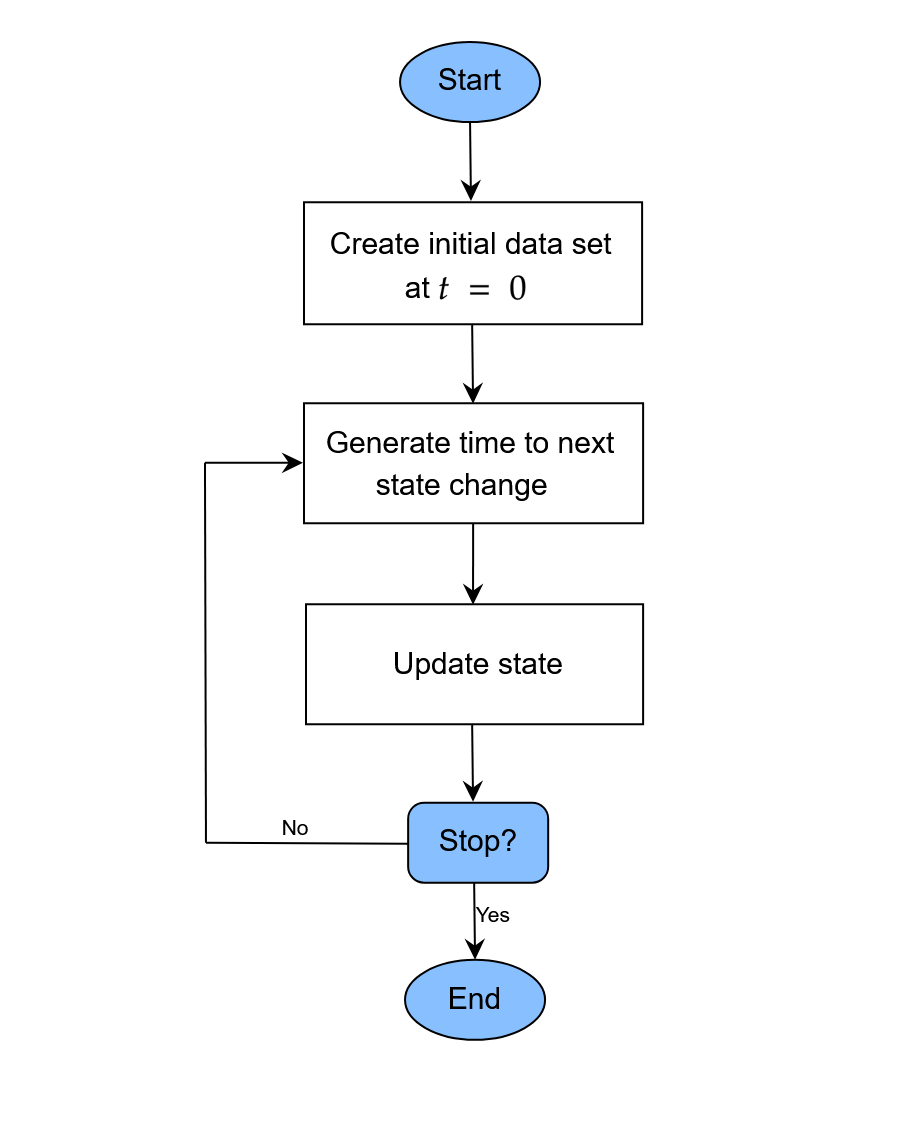
A generalized flow-chart of the discrete-event simulation approach
This approach has many names and usages in the literature. In physics
and chemistry, the particular variant discussed here is known as the
Gillespie algorithm (Gillespie 1976,
1977), or the next reaction or first reaction
method (Anderson 2007). Formally, it is a
mathematically exact method to generate random trajectories from a known
(not necessarily Markovian) stochastic process (Masuda and Rocha 2018). Formal descriptions of
the algorithm are given in the cited literature. The most general
description of the DES (or Gillespie algorithm) implemented in
sim_discrete_event() is as follows for every
individual:
- At
,
initialize the baseline covariate values and set all
time-dependent covariates to
FALSE.
- At
,
initialize the baseline covariate values and set all
time-dependent covariates to
- For each of the considered time-dependent variables, generate the time until the next change based on some distributional assumptions (possibly dependent on any variables contained in the current state)
- Advance the simulation to the minimum of the values drawn in step (2).
- Update the value of the time-dependent variable that generated this event.
- Go back to step (2) and repeat until either some condition is met or no changes are possibly anymore (may happen is every time-dependent variable has reached a terminal state).
The sim_discrete_event() directly implements this
workflow, assuming that individuals (rows in the data) do
not influence each other. A data set at
is either simulated using the sim_from_dag() function or
supplied directly by the user (using the t0_data argument).
This data set is then updated according to the time-dependent nodes
added to the dag using node_td() calls. After
each update, the state of the simulation is saved, so that the final
output is a single dataset in the start-stop format. Below we give a
short example on how this works in practice. We use a similar example to
the one used in the discrete-time simulation vignette, to allow direct
comparisons with the discrete-time approach.
Defining the DAG
As for the other simulation functions in this package, the definition
of a DAG is the first required step. Any amount of time-independent
variables specified using standard node() function calls
are supported. Time-dependent nodes should be specified using the
node_td() function instead. Importantly, for
sim_discrete_event(), only time-dependent nodes of type
"next_time" are supported. For more examples and guidance
on how to generally define a DAG, please consult the other vignettes and
documentation pages of this package.
A single time-dependent variable
For illustrative purposes, we will start with a small comparison of
the discrete-time simulation approach and the discrete-event approach.
Consider that we are interested in simulating the time until
death for
individuals. Lets ignore the influence of any other variables for the
moment and just consider death by itself. Suppose that
death has a fixed probability of 0.01 to occur during each
time-unit.
Discrete-Time approach
In a discrete-time simulation, we would simply draw Bernoulli trials
with a probability of 0.01 at
.
If the trial returns a 1, we are done and save the time. If it returns a
0, we increase
by one and repeat until we are finished. This can be done using the
sim_discrete_time() function using the following code:
library(simDAG)
library(data.table)
set.seed(1234)
dag_dts <- empty_dag() +
node_td("death", type="time_to_event", prob_fun=0.01, event_duration=Inf)
simDTS <- sim_discrete_time(dag_dts, n_sim=10, max_t=10000000,
break_if=all(data$death_event==TRUE))
head(simDTS$data)
#> .id death_event death_time
#> <int> <lgcl> <int>
#> 1: 1 TRUE 98
#> 2: 2 TRUE 20
#> 3: 3 TRUE 13
#> 4: 4 TRUE 112
#> 5: 5 TRUE 36
#> 6: 6 TRUE 54Here, we set the max_t argument to a very large number
and told the function to stop once everyone has died using the
break_if argument. This approach works well, but it is also
incredibly inefficient in this simple example. Since death
has a constant probability of 0.01, we could also simply sample time
values from an exponential distribution with rate=0.01.
This is exactly what will be exploited in the DES approach.
Discrete-Event approach
Since we are only interested in a single variable, which has a terminal state (once you are dead, there is no going back), we only need one time-jump and thus only one iteration in the DES approach, while we needed potentially hundreds or thousands in the discrete-time approach. The following code may be used to implement this:
dag_des <- empty_dag() +
node_td("death", type="next_time", prob_fun=0.01,
event_duration=Inf)
simDES <- sim_discrete_event(dag_des, n_sim=10, target_event="death")
head(simDES)
#> Key: <.id, start>
#> .id start stop death
#> <int> <num> <num> <lgcl>
#> 1: 1 0 103.242570 TRUE
#> 2: 2 0 141.148734 TRUE
#> 3: 3 0 105.549136 TRUE
#> 4: 4 0 92.690158 TRUE
#> 5: 5 0 2.877996 TRUE
#> 6: 6 0 148.742697 TRUEThere are some differences to the output of the
sim_discrete_time() function. First, because we are using
the DES approach, the time is continuous and not discrete. Secondly, the
output is naturally in the start-stop format, because there would be no
other useful way to represent it. Because there is only one change, each
individual only has one row in the dataset and it is thus still almost
equivalent to the output of the discrete-time approach.
In this example the sim_discrete_event() output is
exactly equal to just calling rexp(10, rate=0.01), while
the sim_discrete_time() output is a discrete-time
approximation to it.
Two interrelated time-dependent variables
We will now make the example a little more complex, by including a time-dependent variable which directly influences the probability of death. Consider the following code:
prob_death <- function(data) {
0.001 * 0.8^(data$treatment)
}
dag <- empty_dag() +
node_td("treatment", type="next_time", prob_fun=0.01,
event_duration=100) +
node_td("death", type="next_time", prob_fun=prob_death,
event_duration=Inf)
sim <- sim_discrete_event(dag, n_sim=10, remove_if=death==TRUE,
target_event="death")Here, we specified two time-dependent nodes of type
"next_time". The first one denotes the
treatment, which has a fixed probability of being given to
a person. It then has an effect for 100 time units, after which the
variable turns back to FALSE. Once it is FALSE
again, it may be given to the same person again immediatly, with a
probability of 0.01. The probability of the death of a
person is now no longer fixed, but a function of the
treatment status. The general probability of death is 0.001
per time unit, but it is reduced by a factor of 0.8 if the
treatment is currently in effect.
Importantly, in this simulation we had to use one of the three
arguments that define an end of the simulation: max_t,
remove_if or break_if. We specified
remove_if, so that all individuals who die are no longer
part of the simulation. Alternatively, we could have gotten a similar
effect using the break_if argument, or limit the amount of
time the simulation may run with max_t. The latter is not
very useful here, because we are interested in the time of death. If we
hadn’t used any of these arguments, the simulation would be updated
exactly 1000 times per person (default value of the
max_loops argument), because treatment does
not have a terminal state (both its event_duration and
immunity_duration are finite). The
target_event argument is only used to make the output a
little prettier.
The generated data for the first individual look like this:
head(sim, 9)
#> Key: <.id, start>
#> .id start stop treatment death
#> <int> <num> <num> <lgcl> <lgcl>
#> 1: 1 0.00000 15.65804 FALSE FALSE
#> 2: 1 15.65804 115.65804 TRUE FALSE
#> 3: 1 115.65804 168.33340 FALSE FALSE
#> 4: 1 168.33340 268.33340 TRUE FALSE
#> 5: 1 268.33340 420.23653 FALSE FALSE
#> 6: 1 420.23653 520.23653 TRUE FALSE
#> 7: 1 520.23653 606.02564 FALSE FALSE
#> 8: 1 606.02564 706.02564 TRUE FALSE
#> 9: 1 706.02564 861.85932 FALSE TRUEAs can be seen, the treatment keeps switching between
TRUE and FALSE until the death is
eventually reached. If we increased n_sim and fit a Cox
proportional hazards regression model with the time-to
death as the endpoint and the treatment as
covariate, we would be able to recover the 0.8 as the hazard ratio for
the treatment. The same strategy could of course be used for any amount
of time-varying variables.
Some things to consider
Time-Dependent probabilities and effects
By default, the time until the next event is generated using a random
draw from an exponential distribution. This approach, however, assumes
that the probability of occurrence is independent of the time. We can
relax this assumption by using the redraw_at_t argument.
This argument allows users to specify points in time at which the time
to the next event should be re-drawn. By additionally making the
probability function supplied to a time-dependent node time-specific, we
can then use a piecewise-constant probability instead. Consider the
following code:
prob_death <- function(data) {
base_p <- fifelse(data$.time > 300, 0.005, 0.001)
base_p * 0.8^(data$treatment)
}
dag <- empty_dag() +
node_td("treatment", type="next_time", prob_fun=0.01,
event_duration=100) +
node_td("death", type="next_time", prob_fun=prob_death,
event_duration=Inf)
sim <- sim_discrete_event(dag, n_sim=10, remove_if=death==TRUE,
target_event="death", redraw_at_t=300)
head(sim)
#> Key: <.id, start>
#> .id start stop treatment death
#> <int> <num> <num> <lgcl> <lgcl>
#> 1: 1 0.0000 218.7493 FALSE FALSE
#> 2: 1 218.7493 300.0000 TRUE FALSE
#> 3: 1 300.0000 318.7493 TRUE FALSE
#> 4: 1 318.7493 329.5813 FALSE TRUE
#> 5: 2 0.0000 224.3341 FALSE FALSE
#> 6: 2 224.3341 231.5720 TRUE TRUEIn this code, the baseline probability is 0.001 until
and then increases to 0.005. It is not sufficient to only define the
probability function this way, because then there would be no way for
the simulation itself to know that the event durations have to be
re-drawn. For example, lets say the death time drawn at
for some person is 678 and assume that treatment has no
effect for this individual. This time was generated using a rate of
0.001, so only the time until 300 is valid. At
,
we therefore have to re-draw another time from a truncated exponential
distribution with the new rate of 0.005 (truncated at 300).
The same strategy could be used to define piecewise-constant
time-dependent effects as well. One would only need to adjust the
prob_death() function so that it has a different factor for
treatment depending on the time. Using continuously
changing probabilities is more difficult, but possible. If for example,
we assume that the baseline probability follows a Weibull distribution,
we could use the same algorithm that is used in the
node_cox() function to draw the event times instead. This
could be done by changing the distr_fun argument inside the
relevant node_td() call appropriately.
Categorical / Count / Continuous variables
With the current implementation, only time-dependent variables are
supported. There is no way to easily integrate time-dependent
categorical, count or continuous variables instead. If these are
required, users may need to use the sim_discrete_time()
function.
Ties in event times
Conceptually, no complications arise from multiple events happening
at the same exact time, which we will call ties from here on.
If ties occur, the algorithm should simply update the respective
variables at the same time, generating only one new row for the
start-stop dataset. The simulation may then proceed as usual.
Computationally, it does make a difference though. The
sim_discrete_event() function internally uses a mix of a
long- and wide-format dataset. Updating this dataset is fast and
efficient if it can be assumed that only one event occurs, but somewhat
more involved if we have to allow ties. This is where the
allow_ties argument comes in.
By default, the time until the next event is drawn from a (truncated)
exponential distribution and thus truly continuous. In this case, the
likelihood that two generated event times, lets say for variable
and
are exactly equal are astronomically small. For all intents and
purposes, we may ignore this possibility. The allow_ties
argument is therefore set to FALSE by default, allowing
computations to be a lot faster. If, however, the user supplies a custom
function that generates integer based times, this argument needs to be
set to TRUE (otherwise an error will be returned).
For example, consider the following code:
prob_death <- function(data) {
0.001 * 0.8^(data$treatment)
}
integer_rtexp <- function(n, rate, l) {
ceiling(rtexp(n=n, rate=rate, l=l))
}
dag <- empty_dag() +
node_td("treatment", type="next_time", prob_fun=0.01,
event_duration=100, distr_fun=integer_rtexp) +
node_td("death", type="next_time", prob_fun=prob_death,
event_duration=Inf, distr_fun=integer_rtexp)
sim <- sim_discrete_event(dag, n_sim=1000, remove_if=death==TRUE,
target_event="death", allow_ties=TRUE)Here, we use an artificially discretized version of the truncated
exponential distribution to generate the time until the next change.
This may lead to ties, so we need to set allow_ties=TRUE.
Note that for sample sizes below 10000, the computational differences
are very small. Only with large n_sim does the difference
between allow_ties=TRUE and allow_ties=FALSE
become more noticeable.
Discussion
The sim_discrete_event() function has multiple
advantages over its sibling, the sim_discrete_time()
function. As a general rule, if a DGP can be described in terms of only
binary time-dependent variables (plus an arbitrary amount of
time-constant variable) it should be possibly to use both functions. In
this case, the sim_discrete_event() approach is often much
faster and more efficient and thus preferable. If more complex data is
required, the discrete-time simulation approach offers more flexibility,
while also being easier to understand, at the cost of computational
time.